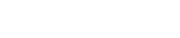Finding optimal rigidity
One common misunderstanding about sandwich structures leads many designers to overestimate overall stiffness or to stiffen sandwich structures in a less than optimal fashion.
In this article, we expose the true behavior of sandwich structures and share the elements of optimal sandwich structure design.
High-stiffness and strength, even in flexion
Because of their high-stiffness and strength, composite panels can be made thin, yet be suited to carry significant in-plane loading. However, because they are thin, these panels will not be very stiff in flexion.
An easy way to remedy this situation is to incorporate a core material within the panel. The core allows the stiff composites to be located further away from the panel’s neutral axis, increasing its flexural stiffness.
The problem with the I-beam theory
Sandwich panels are often compared to I-beams, where the facesheets are homologous to the I-beam’s flanges and the core represents the beam’s web.
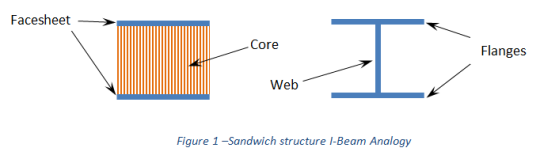
Figure 1 –Sandwich structure I-Beam Analogy
The problem with this analogy is that it does not fully illustrate the relatively low shear stiffness of the core material.
When transverse loads are applied to the sandwich structure (or if transverse shears are otherwise present), the actual deformations will not be predicted correctly unless the core shear stiffness is adequately modelled.
Deflection in an example sandwich structure
For example, let’s consider a sandwich panel (see Figure 2) with a thickness h and facesheets with thickness t. For simplicity, assume the facesheets have a modulus of elasticity E.
If the thickness of the facesheets is small compared to the overall sandwich thickness (t << h), the flexural stiffness per unit length D of the sandwich panel can be approximated by:
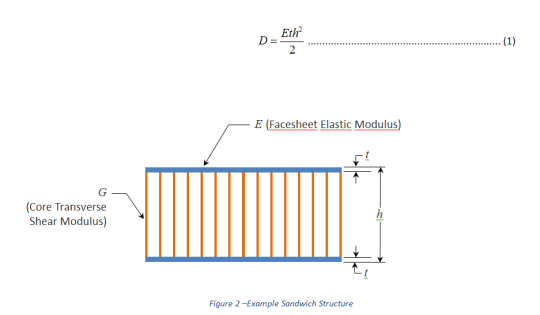
Figure 2 –Example Sandwich Structure
Consider a length d of this sandwich panel arranged as a cantilever beam and loaded vertically at its free end with a force V (see Figure 3).
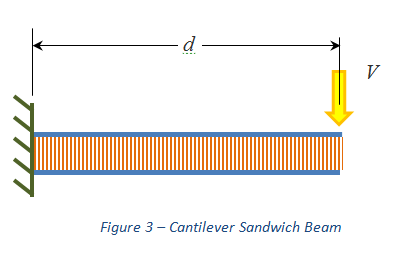
Figure 3 – Cantilever Sandwich Beam
From beam theory, the deflection can be related to a moment M within the beam with:

Since the moment is also related to the applied force V, we have the following differential equation:

Knowing that the beam is rigidly attached at x=0:

The deflection along the beam is obtained as:

And at the tip:

However, when this experiment is performed with typical core materials, one soon discovers that the deflection predicted for the tip of the beam is underestimated. In reality, another component of deflection w’ must be taken into consideration due to the relatively low transverse shear stiffness of the core:

In our example, a constant transverse shear stress is carried throughout the core:

And the additional deflection due to shear can readily be obtained as:

Thus, the total deflection at the tip of the beam becomes:
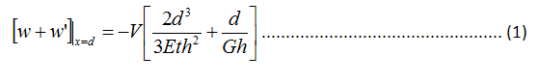
How sandwich structures actually behave
And there, in this last equation, we discover the true behavior of sandwich structures with respect to out-of-plane loading.
Of course, the final equations will vary greatly as a result of the actual problem’s boundary conditions, but the general idea is that three parameters can be altered to increase the flexural rigidity of a sandwich panel. These are:
• Core height
• Core transverse shear stiffness
• Facesheet thickness
Increasing facesheet thickness is the least effective method of achieving a rigid sandwich (not to mention the cost involved, especially when dealing with composites).
In practicality, an optimal sandwich structure will be the result of a judicious combination of core thickness and core stiffness.
The importance of correct shear stiffness values
This exercise also highlights the importance of correctly inputting the core transverse shear stiffness values when performing a finite element analysis.
Using the correct values allows the software to estimate deflections adequately.
Finally, one should always take great care in ensuring that the core transverse shear effects are taken into account when performing buckling analysis of sandwich panels. Read more about approaches to laminate buckling.
Looking for help with a sandwich stiffness problem?