Trouver la rigidité optimale
Un malentendu répandu sur les structures sandwich mène de nombreux concepteurs à surestimer leur rigidité globale ou à les rigidifier d’une façon loin d’être optimale.
Dans cet article, nous expliquons le véritable comportement des structures sandwich et présentons les éléments de la conception optimale de ces structures.
Haute rigidité et résistance, même en flexion
Grâce à leur grande rigidité et leur résistance, les panneaux composites peuvent être fins, mais adaptés pour supporter une charge considérable dans le plan. Cependant, en raison de leur faible épaisseur, ces panneaux ne seront pas très rigides en flexion.
Une façon simple de remédier à cette situation est d’incorporer au panneau un matériau qui en sera l’âme. L’âme permet aux composites rigides d’être situés encore plus loin de l’axe neutre du panneau, ce qui accroît la rigidité à la flexion.
Le problème de la théorie des poutres en I
Les panneaux sandwich sont souvent comparés aux poutres en I : les peaux sont analogues aux brides de la poutre en I et l’âme équivaut à celle de la poutre.
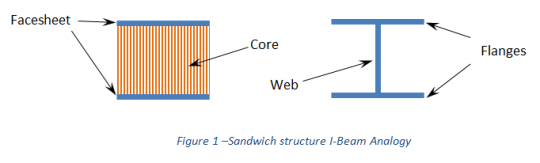
Figure 1 – Analogie entre la structure sandwich et la poutre en I
Le problème de cette analogie est qu’elle ne reflète pas complètement la rigidité au cisaillement relativement faible du matériau de l’âme.
Lorsque des charges transversales sont appliquées à la structure sandwich (ou si des cisaillements transversaux sont présents d’une autre façon), les déformations réelles ne seront pas prévues correctement, sauf si la rigidité au cisaillement de l’âme est adéquatement modélisée.
Déformation dans un exemple de structure sandwich
Prenons par exemple un panneau sandwich (voir Figure 2) avec une épaisseur h et des peaux avec une épaisseur t. Pour simplifier, supposons que les peaux ont un module d’élasticité E.
Si l’épaisseur des peaux est faible par rapport à l’épaisseur globale du sandwich (t << h), la rigidité à la flexion par unité de longueur D du panneau sandwich peut être calculée par approximation de la façon suivante :
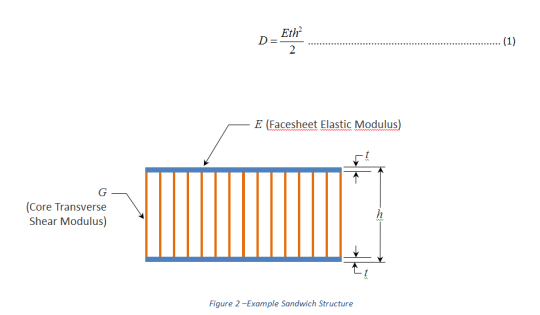
Figure 2 – Exemple de structure sandwich
Prenons une longueur d de ce panneau sandwich disposé comme une poutre en porte-à-faux, auquel est appliquée verticalement une force V à son extrémité libre (voir Figure 3).
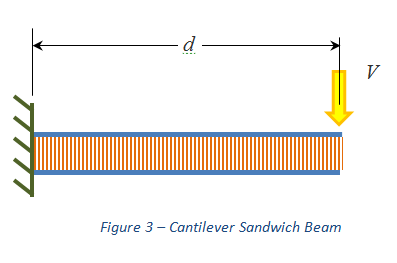
Figure 3 – Poutre sandwich en porte-à-faux
D’après la théorie des poutres, la déformation peut être relative à un moment M dans la poutre avec :

Dans la mesure où le moment est également relatif à la force appliquée V, nous avons l’équation différentielle suivante :

Sachant que la poutre est rigidement fixée à x=0 :

La déformation le long de la poutre est obtenue comme suit :

Et à l’extrémité :

Cependant, lorsque cette expérience est réalisée avec les matériaux d’âme habituels, on découvre rapidement que la déformation prévue à l’extrémité de la poutre est sous-estimée.
En réalité, un autre composant de la déformation w’ doit être pris en compte, en raison de la rigidité au cisaillement transversal relativement faible de l’âme :

Dans notre exemple, une contrainte de cisaillement transversale constante est appliquée tout au long de l’âme :

Et la déformation supplémentaire due au cisaillement peut facilement être obtenue comme suit :

Par conséquent, la déformation totale à l’extrémité de la poutre devient :
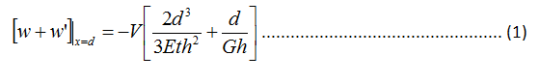
Comment les structures sandwich se comportent réellement
Et ici, avec cette dernière équation, nous découvrons le comportement véritable des structures sandwich en ce qui concerne la charge hors plan.
Bien sûr, les équations finales varieront fortement en raison des conditions limites du problème réel, mais l’idée générale est que ces trois paramètres peuvent être modifiés pour accroître la rigidité à la flexion d’un panneau sandwich. Il s’agit des paramètres suivants :
- Hauteur de l’âme
- Rigidité au cisaillement transversal de l’âme
- Épaisseur de la peau
Augmenter l’épaisseur de la peau est la méthode la moins efficace pour obtenir un sandwich rigide (sans compter le coût impliqué, notamment lorsqu’il s’agit de composites).
En pratique, une structure sandwich optimale sera le résultat d’une combinaison judicieuse d’une épaisseur et d’une rigidité de l’âme.
L’importance des valeurs correctes de rigidité au cisaillement
Cet exercice souligne également l’importance de saisir correctement les valeurs de rigidité au cisaillement transversal de l’âme lors de la réalisation d’une analyse sur un élément fini.
Utiliser les bonnes valeurs permet au logiciel d’estimer adéquatement les déformations.
Enfin, il faut toujours être particulièrement vigilant pour assurer que les effets de cisaillement transversal sont pris en compte lors de la réalisation d’une analyse de flambage des panneaux sandwich. En savoir plus sur les approches du flambage des matériaux laminés.
Vous avez besoin d’aide sur un problème de rigidité de sandwich ?