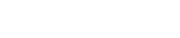How to know which one applies
Understand the difference between the failure index and strength ratio, and how each should be applied when using composite material quadratic failure criteria.
The relationship between failure and strength in uniaxial loading
In a uniaxial loading situation, failure prediction is reduced to a comparison of the internal stresses (s) to the material’s strength (F) in the loading direction.
In such a case, the failure index (FI) and the strength ratio (R) are defined as:
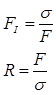
In this simple scenario, the failure index and strength ratio are clearly inversely related.
Extending this example to a composite material layer (Figure 1) and comparing each component of the stress state to the material strength properties, one can draw the ply failure envelope for the maximum stress criterion (Figure 2).
Figure 1 – Composite Layer Stress State
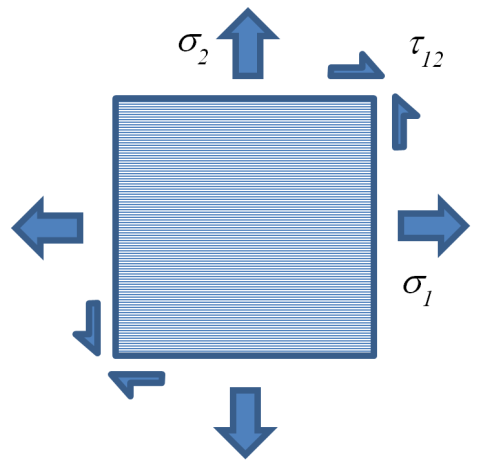
Figure 2 – Maximum Stress Ply Failure Envelope
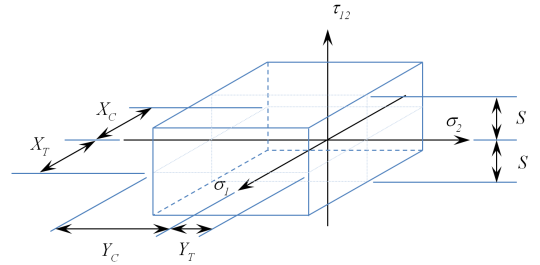
XT: Tension Allowable in 1-direction
XC: Compression Allowable in 1-direction
YT: Tension Allowable in 2-direction
YC: Compression Allowable in 2-direction
S: In-Plane Shear Allowable
A stress state example
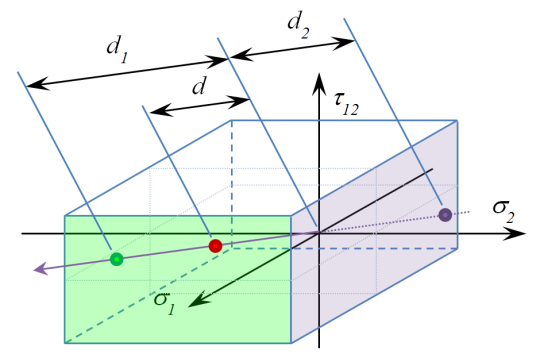
A stress state (the red dot in Figure 3) contained within the envelope is considered to be within the acceptable limits of the material. This stress state, multiplied by a positive value (d1/d=R), would eventually cross the envelope boundary (the green dot).
Because the envelope is a finite volume, the boundary can also be reached if the stress state is multiplied by a negative number (-d2/d) (the purple dot).
This point, while mathematically correct, is usually neglected, as it does not represent the exaggerated physical stress state.
Figure 3 – Stress State within the Ply Failure Envelope
Quadratic ply failure
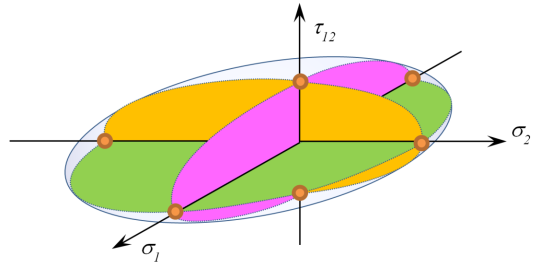
The same reasoning applies to other failure criteria, such as the quadratic failure envelope family. A typical quadratic ply failure envelope is illustrated in Figure 4.
Figure 4 – Quadratic Ply Failure Envelope
A quadratic failure envelope boundary can be defined within a single equation.
For example, the Hill failure envelope can be expressed as:
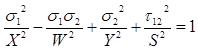
With:
(2)
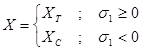
(3)
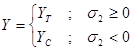
(4)
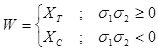
(5)
If the stress state is contained within the volume surrounded by the ply failure envelope, no failure is predicted.
One would still like to know by what strength ratio R the stresses can be multiplied so as to cross the envelope, producing failure. Simply multiplying all the stresses from the Hill failure envelope by the value R yields an expression that can readily be solved:
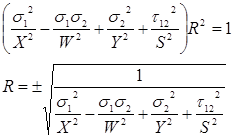
(6)
From this, only the positive value is retained.
In this case, it makes sense to define the ply failure index as:
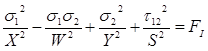
(7)
Yielding the relationship:
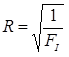
(8)
Clearly, failure can be ascertained when the failure index has a value of 1 (ply envelope boundary) or above. A value between 0 and 1 will also provide an indication of how close to failure is the ply.
If one instead uses the Tsai-Wu Failure criterion:
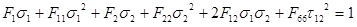
With:
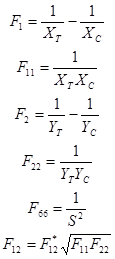
(10)
And F*12 is a user-defined interaction coefficient.
The strength ratio can be obtained by solving the following equation:
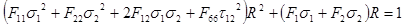
Note that some terms are of second order while others are not. Solving and keeping only the positive root yields:
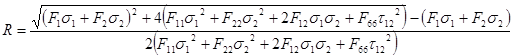
Now, for consistency with the other quadratic failure criteria (and for historical reasons), the Tsai-Wu failure index is defined as:
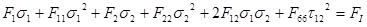
Is there a relationship between failure index and strength ratio?
In this case, there is no direct relationship between the failure index and the strength ratio.
The failure index cannot provide valuable insight on failure unless it has a value of 1. In fact, depending on the stress values, it is even possible to obtain a negative failure index.
As a rule of thumb, whenever a failure criterion involves mixed order terms (e.g., Tsai-Wu), there will be no relationship between the failure index and the strength ratio. In these situations, failure predictions should be based on the strength ratio.
Composite material expertise
Read more:
The stiffness of sandwich structures
Approaches to laminate buckling
Tackling complex composite material problems? We can help.