Comment savoir lequel s’applique
Comprenez la différence entre l’indice de défaillance et le coefficient de résistance, et comment chacun d’eux doit être appliqué en cas d’utilisation d’un critère de défaillance quadratique des matériaux composites.
La relation entre défaillance et résistance dans une charge uniaxiale
Dans une situation de charge uniaxiale, la prévision de défaillance est réduite à une comparaison des contraintes internes (s) et de la résistance du matériau (F) dans la direction de charge.
Dans ce cas, l’indice de défaillance (FI) et le coefficient de résistance (R) sont définis comme suit :
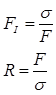
Dans ce scénario simple, l’indice de défaillance et le coefficient de résistance sont clairement inversement proportionnels.
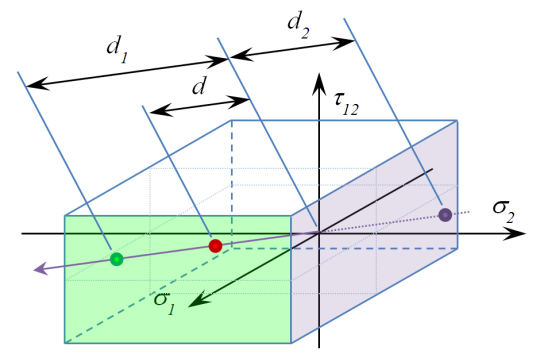
En étendant cet exemple à une couche de matériau composite (Figure 1) et en comparant chaque composante de l’état de contrainte aux propriétés de résistance du matériau, on peut dessiner l’enveloppe de défaillance de pli pour le critère de contrainte maximale (Figure 2).
Figure 1 – État de contrainte de la couche composite
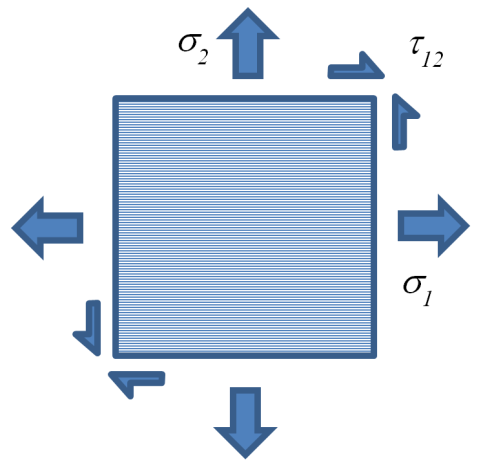
Figure 2 – Enveloppe de défaillance de pli pour la contrainte maximale
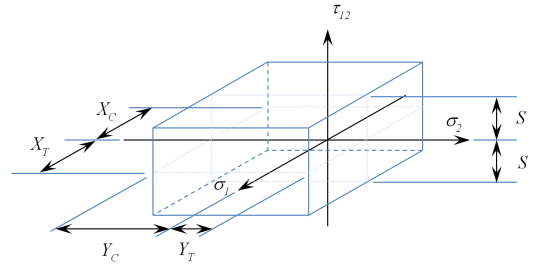
XT : Contrainte admissible dans une direction
XC : Compression admissible dans une direction
YT : Contrainte admissible dans deux directions
YC : Compression admissible dans deux directions
S : Cisaillement admissible dans le plan
Un exemple d’état de contrainte
Un état de contrainte (point rouge dans la Figure 3) compris dans l’enveloppe est considéré comme dans les limites acceptables du matériau. S’il est multiplié par une valeur positive (d1/d=R), cet état de contrainte finira par passer la limite de l’enveloppe (point vert).
Comme l’enveloppe est un volume fini, la limite peut également être atteinte si l’état de contrainte est multiplié par un nombre négatif (-d2/d) (point violet).
S’il est mathématiquement correct, ce point est généralement négligé, car il ne représente pas l’état de contrainte physique exagéré.
Figure 3 – État de contrainte dans les limites de l’enveloppe de défaillance de pli
Défaillance quadratique du pli
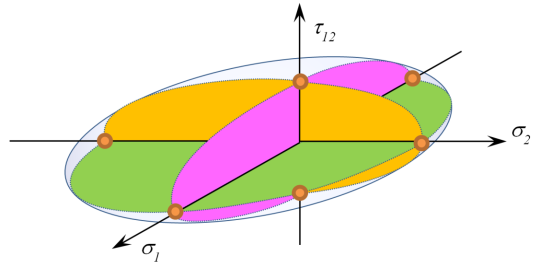
Le même raisonnement s’applique à d’autres critères de défaillance, comme ceux de la famille de l’enveloppe de défaillance quadratique. Une enveloppe typique de défaillance quadratique de pli est illustrée à la Figure 4.
Figure 4 – Enveloppe de défaillance quadratique de pli
Une limite d’enveloppe de défaillance quadratique peut être définie avec une simple équation.
Par exemple, l’enveloppe de défaillance de Hill peut être exprimée comme suit :
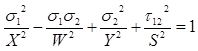
Avec :
(2)
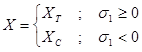
(3)
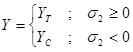
(4)
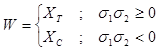
(5)
Si l’état de contrainte est contenu dans le volume entouré par l’enveloppe de défaillance de pli, aucune défaillance n’est prévue.
On souhaiterait tout de même savoir par quel coefficient de résistance R les contraintes peuvent être multipliées pour passer l’enveloppe, ce qui produit une défaillance. Multiplier simplement toutes les contraintes de l’enveloppe de défaillance de Hill par la valeur R donne une expression qui peut être rapidement résolue :
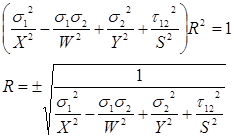
(6)
À partir de cela, seule la valeur positive est retenue.
Dans ce cas, il est judicieux de définir l’indice de défaillance de pli comme suit :
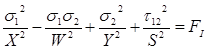
(7)
Ce qui donne la relation :
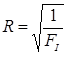
(8)
Clairement, la défaillance peut être établie quand l’indice de défaillance a une valeur de 1 (limite de l’enveloppe de pli) ou supérieure. Une valeur comprise entre 0 et 1 indiquera également dans quelle mesure la défaillance de pli est proche.
Si l’on utilise plutôt le critère de défaillance de Tsai-Wu :
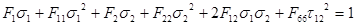
Avec :
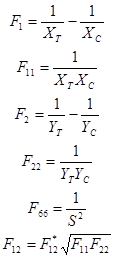
(10)
F*12 est un coefficient d’interaction défini par l’utilisateur. Le coefficient de résistance peut être obtenu grâce à la résolution de l’équation suivante :
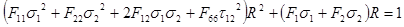
Veuillez noter que certains termes sont du second ordre, tandis que d’autres ne le sont pas. Résoudre et conserver uniquement les racines carrées positives donne :
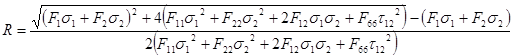
Cela dit, à des fins de cohérence avec l’autre critère de défaillance quadratique (et pour des raisons historiques), l’indice de défaillance de Tsai-Wu est défini comme suit :
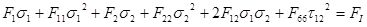
Existe-t-il une relation entre l’indice de défaillance et le coefficient de résistance ?
Dans ce cas, il n’y a pas de relation directe entre l’indice de défaillance et le coefficient de résistance.
L’indice de défaillance ne peut pas fournir d’informations utiles sur la défaillance, à moins qu’il n’ait une valeur de 1. En fait, selon les valeurs de résistance, il est même possible d’obtenir un indice de défaillance négatif.
En règle générale, chaque fois qu’un critère de défaillance implique des termes de type mixte (par ex. Tsai-Wu), il n’y aura pas de relation entre l’indice de défaillance et le coefficient de résistance. Dans ces situations, les prévisions de défaillance doivent être fondées sur le coefficient de résistance.
Expertise sur les matériaux composites
En savoir plus :
Vous vous attaquez à des problèmes complexes de matériaux composites ? Nous pouvons vous aider.
Contactez un expert Maya HTT dès aujourd’hui.